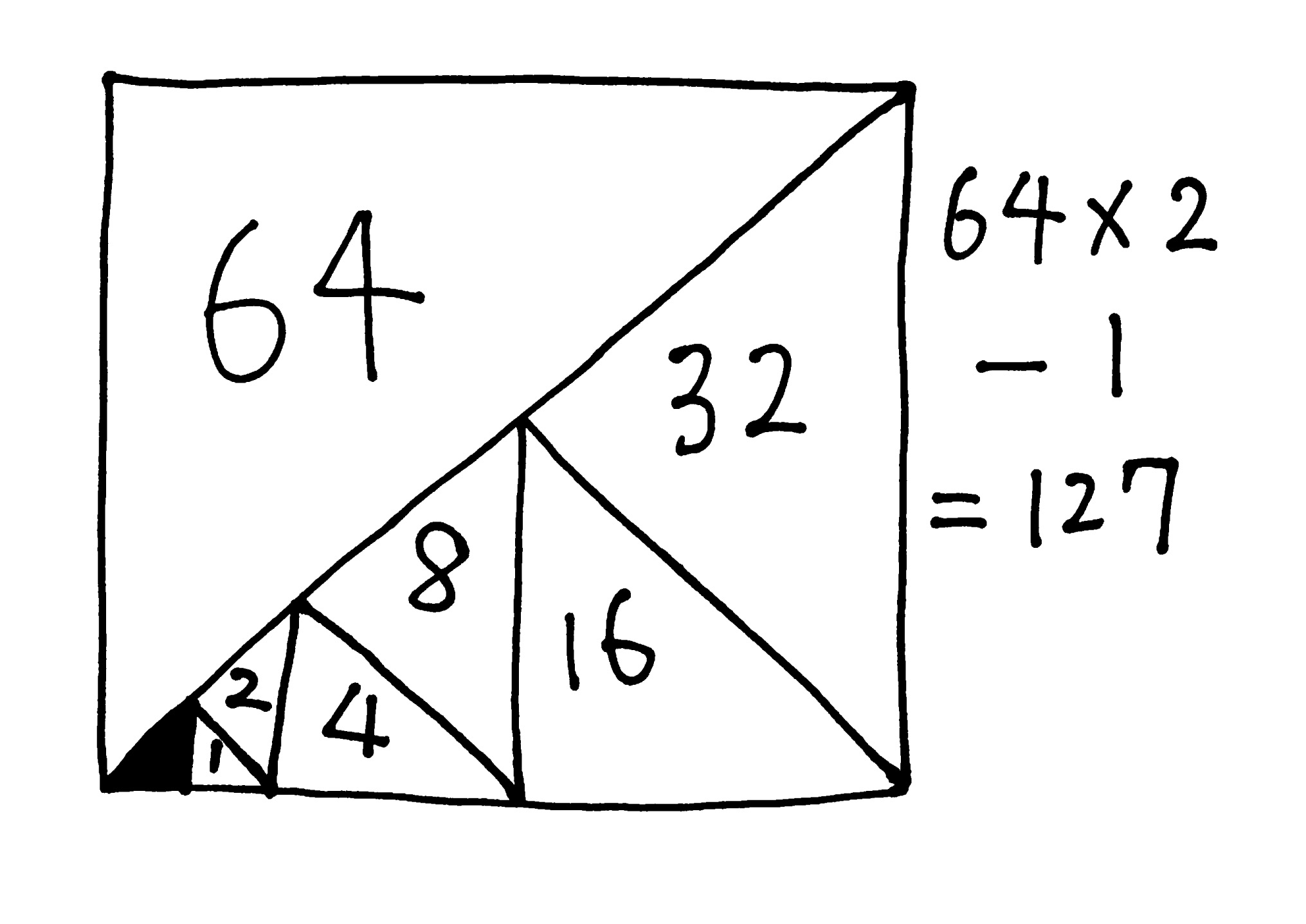【昔の中学受験】（雑談）　美しい算数

本ブログの目次はコチラ。

本ブログではここまで国語について話すことが多かったのですが、私が得意だったのは算数、数学でした。最初、武蔵を目指していたこともあって、美しい算数の解き方にあこがれを持っていました。

私が小学校4年生の時の話です。まだ塾にも通っていない頃でした。

中学生の兄が、昼寝している私を起こして、次のような問題を出してきました。

（問）1+2+4+8+16+32+64=?

眠い目をこすりながら、「64を2倍して、1を引けばいいよ」と私は口頭で答えました（←コレ、本当の話です）。どうやって考えたか分かります？

これは等比数列の和を求める問題で、中高生が数学で習う問題です。一般的には以下のように解きます。

式①：S(合計という意味）＝1+2+4+8+16+32+64

式②：2×S=(1+2+4+8+16+32+64)×2=2+4+8+16+32+64+128

と並べて、式②と式①を見比べて引き算をすると、共通する数字は消えるので

式②ー式①：2×S – S=128-1=127

となります。

小学校4年生の私は数学など知らなかったのですが、以下のような図形がパッと頭に浮かびました。

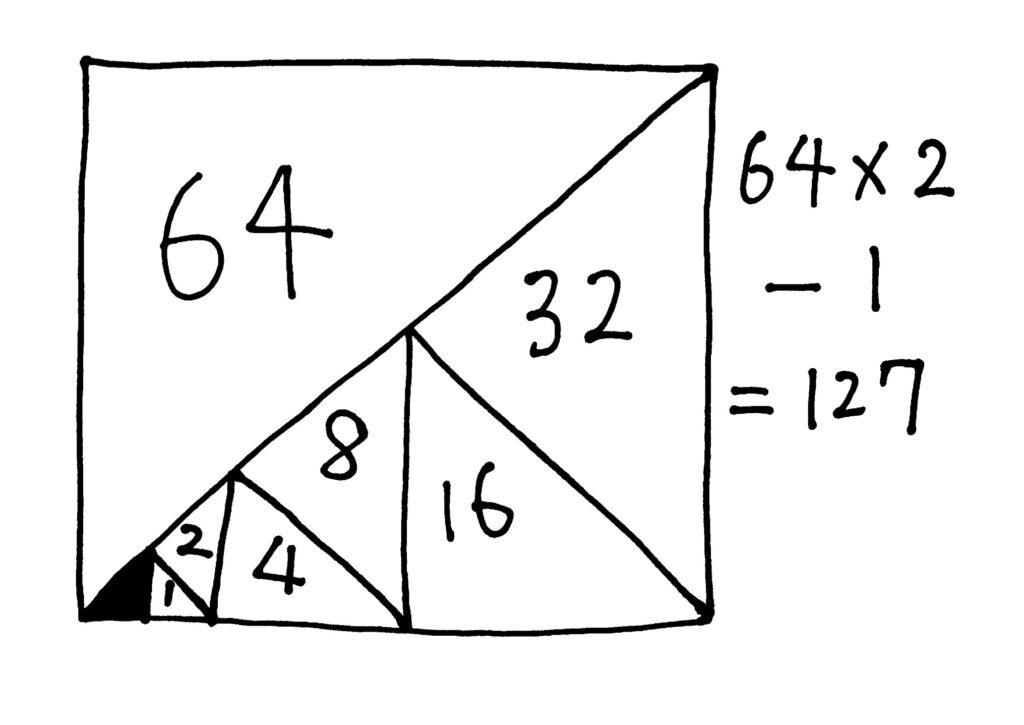
面積が2倍の直角二等辺三角形を複数集めると、正方形ができます（こういう知育パズルは最近多いですよね）。全体の面積は当然、一番大きい直角二等辺三角形の面積（=64）の2倍（=128）です。でもよく見ると、一番小さい直角二等辺三角形1個分（図の黒いところ）が埋まっていません。だから「－1」をするのです。

この解き方の難点は、×3や×4などの×2以外の等比数列の和を求めるには応用できないところです。でもきれいな解き方だと思いません？中学受験の参考書はたくさんありますが、どの本にも掲載されていないと思います。

いかに、先生が思いつかない解法を見つけるか？当時、そんなことばかり考えていました。

以前、開成の算数はただただ疲れる、と書きましたが、今でも美しい算数が残っている学校があると、息子の中学入試勉強を見ながら思いました。。。それは、、、麻布と灘です。（注）個人の感想です。が、同意してくれる方は多いと思います。